Big ideas math modeling real life grade 7 delves into the fascinating world of mathematical modeling, where students discover how math transcends textbooks and plays a pivotal role in solving real-world problems. This engaging exploration unveils the types of mathematical models used in grade 7, the steps involved in creating them, and the limitations they may encounter.
By harnessing technology and engaging in hands-on projects, students gain a deeper understanding of how mathematical modeling empowers them to make predictions, optimize solutions, and contribute to meaningful decision-making.
Throughout this journey, students will encounter linear, exponential, and quadratic models, each with unique applications. They will learn the importance of problem identification, data collection, model development, and validation, ensuring the accuracy and reliability of their models. Furthermore, they will explore the role of technology in enhancing the modeling process, using spreadsheets, graphing calculators, and specialized software to streamline analysis and visualization.
1. Real-Life Applications of Mathematical Modeling
Mathematical modeling plays a crucial role in solving real-life problems across various fields. By creating mathematical models that represent real-world situations, scientists, engineers, and researchers can make predictions, optimize solutions, and gain insights into complex phenomena.
Examples of Mathematical Modeling in Real Life:
- Predicting population growth to plan for future infrastructure and resource allocation.
- Optimizing travel routes to reduce travel time and fuel consumption.
- Designing structures such as bridges and buildings to withstand forces and ensure safety.
- Modeling financial markets to predict trends and make informed investment decisions.
- Simulating weather patterns to forecast weather events and mitigate their impact.
2. Types of Mathematical Models in Grade 7
In grade 7, students encounter various types of mathematical models, each with unique characteristics and applications.
Linear Models:
Linear models represent relationships between two variables that change at a constant rate. They are expressed as equations of the form y = mx + b, where m is the slope and b is the y-intercept. Linear models are used to model population growth, predict trends, and optimize resource allocation.
Exponential Models:
Exponential models represent relationships between two variables that change at a constant percentage rate. They are expressed as equations of the form y = ab^x, where a is the initial value and b is the growth factor. Exponential models are used to model population growth, radioactive decay, and compound interest.
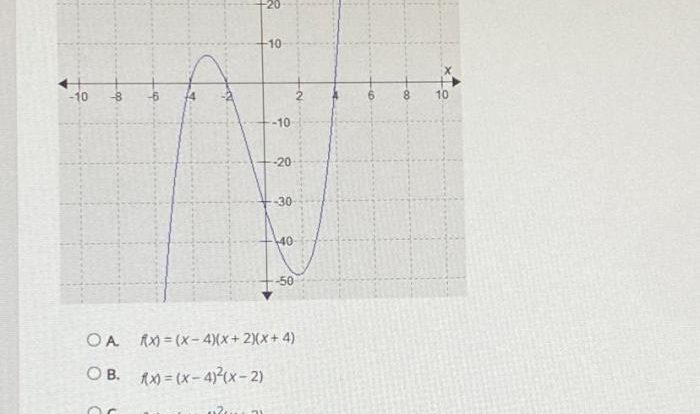
Quadratic Models:
Quadratic models represent relationships between two variables that change at a varying rate. They are expressed as equations of the form y = ax^2 + bx + c. Quadratic models are used to model projectile motion, design parabolic structures, and optimize manufacturing processes.
3. Steps in Creating a Mathematical Model
Creating a mathematical model involves a systematic process to ensure accuracy and validity.
Problem Identification:
Clearly define the real-world problem that the model will address.
Data Collection:
Gather relevant data from reliable sources to represent the real-world situation.
Model Development:, Big ideas math modeling real life grade 7
Choose the appropriate mathematical model type and develop an equation that represents the relationship between the variables.
Validation:
Test the model using additional data or compare its predictions to known outcomes to assess its accuracy.
4. Limitations of Mathematical Models

Mathematical models have limitations that must be considered when using them for decision-making.
Assumptions and Simplifications:
Models often make simplifying assumptions to make them manageable. These assumptions may introduce errors into the model’s predictions.
Potential Errors:
Models are only as accurate as the data they are based on and the assumptions made during their development. Errors in data or assumptions can lead to incorrect predictions.
Contextual Factors:
Models may not account for all factors that influence the real-world situation. This can limit their ability to make accurate predictions in complex systems.
5. Using Technology for Mathematical Modeling
Technology plays a vital role in mathematical modeling, enhancing the process of model development and analysis.
Spreadsheets:
Spreadsheets allow for easy data manipulation, equation solving, and graphical representation of models.
Graphing Calculators:
Graphing calculators enable students to visualize models, explore different scenarios, and make predictions.
Modeling Software:
Specialized modeling software provides advanced tools for model development, simulation, and optimization.
6. Examples of Mathematical Modeling Projects: Big Ideas Math Modeling Real Life Grade 7
Mathematical modeling projects provide students with hands-on experience in applying mathematical models to real-world problems.
Project Details:
| Project | Objective | Outcome |
|---|---|---|
| Predicting Population Growth | Use a linear model to predict the future population of a city. | Students will gain insights into population trends and resource planning. |
| Optimizing Travel Routes | Use a quadratic model to design the shortest route between multiple destinations. | Students will learn to optimize travel efficiency and minimize travel time. |
| Designing a Parabolic Bridge | Use a quadratic model to design a parabolic bridge that meets specific structural requirements. | Students will apply mathematical modeling to solve engineering problems. |
Query Resolution
What is mathematical modeling?
Mathematical modeling is the process of creating a mathematical representation of a real-world situation to analyze, make predictions, and solve problems.
What are the different types of mathematical models used in grade 7?
Common types of mathematical models used in grade 7 include linear, exponential, and quadratic models.
What are the steps involved in creating a mathematical model?
The steps involved in creating a mathematical model typically include problem identification, data collection, model development, and validation.
What are the limitations of mathematical models?
Mathematical models have limitations, such as assumptions, simplifications, and potential errors, which can affect their accuracy and reliability.
How can technology be used in mathematical modeling?
Technology, such as spreadsheets, graphing calculators, and modeling software, can enhance the process of model development and analysis.